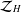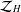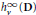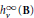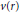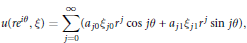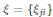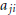In this paper we study a class ${\mathcal{Z}}_{H}$ of harmonic mappings on the open unit disk $\mathbb{D}$ in the complex plane that is an extension of the classical (analytic) Zygmund space. We extend to the elements of this class a characterisation that is valid in the analytic case. We also provide a similar result for a closed separable subspace of ${\mathcal{Z}}_{H}$ which we call the little harmonic Zygmund space.

In this article, we provide a complete description of the spectra of linear fractional composition operators acting on the growth space and Bloch space over the upper half-plane. In addition, we also prove that the norm, essential norm, spectral radius and essential spectral radius of a composition operator acting on the growth space are all equal.

Let 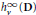$h_{\vee }^{\infty }\,\left( \text{B} \right)$ and 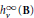$h_{\vee }^{\infty }\,\left( \text{B} \right)$ be the spaces of harmonic functions in the unit disk and multidimensional unit ball admitting a two-sided radial majorant 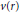$v\left( r \right)$. We consider functions $v$ that fulfill a doubling condition. In the two-dimensional case let

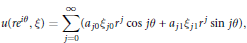$$u\left( r{{e}^{i\theta }},\xi \right)\,=\,\sum\limits_{j=0}^{\infty }{\left( {{a}_{j0}}{{\xi }_{j0}}{{r}^{j}}\,\cos \,j\theta \,+\,{{a}_{j1}}{{\xi }_{j1}}{{r}^{j}}\,\sin \,j\theta \right)}$$

where 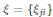$\xi \,=\,\left\{ {{\xi }_{ji}} \right\}$ is a sequence of random subnormal variables and 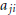${{a}_{ji}}$ are real. In higher dimensions we consider series of spherical harmonics. We will obtain conditions on the coefficients 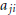${{a}_{ji}}$ that imply that $u$ is in 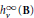$h_{\vee }^{\infty }\,\left( \text{B} \right)$ almost surely. Our estimate improves previous results by Bennett, Stegenga, and Timoney, and we prove that the estimate is sharp. The results for growth spaces can easily be applied to Bloch-type spaces, and we obtain a similar characterization for these spaces that generalizes results by Anderson, Clunie, and Pommerenke and by Guo and Liu.