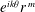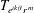1 results
QUASIHOMOGENEOUS TOEPLITZ OPERATORS WITH INTEGRABLE SYMBOLS ON THE HARMONIC BERGMAN SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 494-503
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
-
In this paper, we completely determine the commutativity of two Toeplitz operators on the harmonic Bergman space with integrable quasihomogeneous symbols, one of which is of the form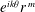
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}e^{ik\theta }r^{\, {m}}$. As an application, the problem of when their product is again a Toeplitz operator is solved. In particular, Toeplitz operators with bounded symbols on the harmonic Bergman space commute with 
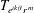$T_{e^{ik\theta }r^{\, {m}}}$ only in trivial cases, which appears quite different from results on analytic Bergman space in Čučković and Rao [‘Mellin transform, monomial symbols, and commuting Toeplitz operators’, J. Funct. Anal.154 (1998), 195–214].
