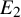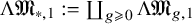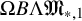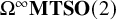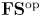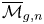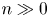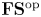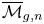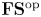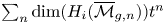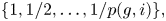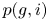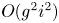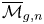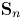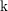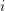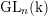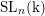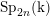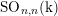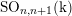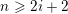Cohomological and motivic inclusion–exclusion
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2228-2283
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Parametrised moduli spaces of surfaces as infinite loop spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability in the homology of Deligne–Mumford compactifications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 17 December 2021, pp. 2635-2656
- Print publication:
- December 2021
-
- Article
- Export citation
Homological vanishing for the Steinberg representation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 1111-1130
- Print publication:
- June 2018
-
- Article
- Export citation
ORBISPACES, CONFIGURATIONS AND QUASI-FIBRATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 August 2016, p. 342
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Twisted homological stability for extensions and automorphism groups of free nilpotent groups
-
- Journal:
- Journal of K-Theory / Volume 14 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 185-201
- Print publication:
- August 2014
-
- Article
- Export citation