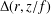Refine search
Actions for selected content:
18 results
Moments of the free Jacobi process: A matrix approach
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 966-991
- Print publication:
- September 2025
-
- Article
- Export citation
New aspects of Bargmann transform using Touchard polynomials and hypergeometric functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-46
-
- Article
- Export citation
Generating function of multiple polylog of Hurwitz type
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 November 2022, pp. 1-17
- Print publication:
- February 2024
-
- Article
- Export citation
ASYMPTOTICS OF A GAUSS HYPERGEOMETRIC FUNCTION WITH TWO LARGE PARAMETERS: A NEW CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 446-452
-
- Article
- Export citation
Mathematical Models for the Propagation of Stress Waves in Elastic Rods: Exact Solutions and Numerical Simulation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 257-270
- Print publication:
- April 2016
-
- Article
- Export citation
INTEGRAL MEANS AND DIRICHLET INTEGRAL FOR CERTAIN CLASSES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 July 2015, pp. 315-333
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A mirror theorem for toric stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1878-1912
- Print publication:
- October 2015
-
- Article
-
- You have access
- Open access
- Export citation
Densities of Short Uniform Random Walks
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 5 / 01 October 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-990
- Print publication:
- 01 October 2012
-
- Article
-
- You have access
- Export citation
THE ACTION OF HECKE OPERATORS ON HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 21 September 2010, pp. 51-74
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Singularities of hypergeometric functions in several variables
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 21 April 2005, pp. 787-810
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation
INVERSE FACTORIAL-SERIES SOLUTIONS OF DIFFERENCE EQUATIONS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 47 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 01 July 2004, pp. 421-448
-
- Article
-
- You have access
- Export citation
Resolution of Some Open Problems Concerning Multiple Zeta Evaluations of Arbitrary Depth
-
- Journal:
- Compositio Mathematica / Volume 139 / Issue 1 / October 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 85-100
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Rational Hypergeometric Functions
-
- Journal:
- Compositio Mathematica / Volume 128 / Issue 2 / September 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 217-240
- Print publication:
- September 2001
-
- Article
-
- You have access
- Export citation
Steady state solution of a single-server queue with linear repeated requests
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 223-233
- Print publication:
- March 1997
-
- Article
- Export citation
Rotational versions of the Crofton formula
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 87-96
- Print publication:
- March 1995
-
- Article
- Export citation
On certain methods of solving a class of integral equations of Fredholm type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-10
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation
Associated Continuous Hahn Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 6 / 01 December 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1263-1280
- Print publication:
- 01 December 1991
-
- Article
-
- You have access
- Export citation
Two Families of Associated Wilson Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 42 / Issue 4 / 01 August 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 659-695
- Print publication:
- 01 August 1990
-
- Article
-
- You have access
- Export citation