1 results
A Buchholz derivation system for the ordinal analysis of KP + Π3-reflection
-
- Journal:
- The Journal of Symbolic Logic / Volume 71 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1237-1283
- Print publication:
- December 2006
-
- Article
- Export citation
-
In this paper we introduce a notation system for the infinitary derivations occurring in the ordinal analysis of KP + Π3-Reflection due to Michael Rathjen. This allows a finitary ordinal analysis of KP + Π3-Reflection. The method used is an extension of techniques developed by Wilfried Buchholz, namely operator controlled notation systems for RS∞-derivations. Similarly to Buchholz we obtain a characterisation of the provably recursive functions of KP + Π3-Reflection as <-recursive functions where < is the ordering on Rathjen's ordinal notation system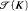
. Further we show a conservation result for 
-sentences.
. Further we show a conservation result for 
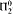-sentences.