W. Casselman defined a basis 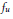 ${{f}_{u}}$ of Iwahori fixed vectors of a spherical representation
${{f}_{u}}$ of Iwahori fixed vectors of a spherical representation 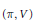 $(\pi ,\,V)$ of a split semisimple
$(\pi ,\,V)$ of a split semisimple 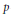 $p$-adic group
$p$-adic group 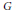 $G$ over a nonarchimedean local field
$G$ over a nonarchimedean local field 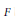 $F$ by the condition that it be dual to the intertwining operators, indexed by elements
$F$ by the condition that it be dual to the intertwining operators, indexed by elements 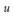 $u$ of the Weyl group
$u$ of the Weyl group 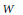 $W$. On the other hand, there is a natural basis
$W$. On the other hand, there is a natural basis 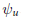 ${{\psi }_{u}}$, and one seeks to find the transition matrices between the two bases. Thus, let
${{\psi }_{u}}$, and one seeks to find the transition matrices between the two bases. Thus, let 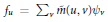 ${{f}_{u}}\,=\,{{\sum }_{v}}\overset{\tilde{\ }}{\mathop{m}}\,(u,\,v){{\psi }_{v}}$ and
${{f}_{u}}\,=\,{{\sum }_{v}}\overset{\tilde{\ }}{\mathop{m}}\,(u,\,v){{\psi }_{v}}$ and 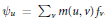 ${{\psi }_{u}}\,=\,{{\sum }_{v}}m(u,\,v){{f}_{v}}$. Using the Iwahori–Hecke algebra we prove that if a combinatorial condition is satisfied, then
${{\psi }_{u}}\,=\,{{\sum }_{v}}m(u,\,v){{f}_{v}}$. Using the Iwahori–Hecke algebra we prove that if a combinatorial condition is satisfied, then 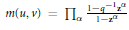 $m(u,\,v)\,=\,{{\Pi }_{\alpha }}\,\frac{1-{{q}^{-1}}\,{{z}^{\alpha }}}{1-{{z}^{\alpha }}}$ , where
$m(u,\,v)\,=\,{{\Pi }_{\alpha }}\,\frac{1-{{q}^{-1}}\,{{z}^{\alpha }}}{1-{{z}^{\alpha }}}$ , where 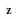 $\mathbf{z}$ are the Langlands parameters for the representation and
$\mathbf{z}$ are the Langlands parameters for the representation and 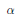 $\alpha $ runs through the set
$\alpha $ runs through the set 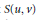 $S(u,\,v)$ of positive coroots
$S(u,\,v)$ of positive coroots 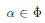 $\alpha \,\in \,\hat{\Phi }$ (the dual root systemof
$\alpha \,\in \,\hat{\Phi }$ (the dual root systemof 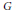 $G$) such that
$G$) such that 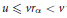 $u\,\le \,v{{r}_{\alpha }}\,<\,v$ with
$u\,\le \,v{{r}_{\alpha }}\,<\,v$ with 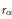 ${{r}_{\alpha }}$ the reflection corresponding to
${{r}_{\alpha }}$ the reflection corresponding to 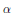 $\alpha $. The condition is conjecturally always satisfied if
$\alpha $. The condition is conjecturally always satisfied if 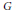 $G$ is simply-laced and the Kazhdan–Lusztig polynomial
$G$ is simply-laced and the Kazhdan–Lusztig polynomial 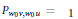 ${{P}_{{{w}_{0}}v,\,{{w}_{0}}u}}\,=\,1$ with
${{P}_{{{w}_{0}}v,\,{{w}_{0}}u}}\,=\,1$ with 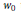 ${{w}_{0}}$ the long Weyl group element. There is a similar formula for
${{w}_{0}}$ the long Weyl group element. There is a similar formula for 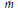 $\tilde{m}$ conjecturally satisfied if
$\tilde{m}$ conjecturally satisfied if 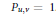 ${{P}_{u,\,v}}\,=\,1$. This leads to various combinatorial conjectures.
${{P}_{u,\,v}}\,=\,1$. This leads to various combinatorial conjectures.