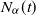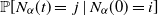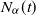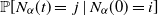In this article we provide new results for the asymptotic behavior of a time-fractional birth and death process $N_{\alpha}(t)$ , whose transition probabilities $\mathbb{P}[N_{\alpha}(t)=\,j\mid N_{\alpha}(0)=i]$ are governed by a time-fractional system of differential equations, under the condition that it is not killed. More specifically, we prove that the concepts of quasi-limiting distribution and quasi-stationary distribution do not coincide, which is a consequence of the long-memory nature of the process. In addition, exact formulas for the quasi-limiting distribution and its rate convergence are presented. In the first sections, we revisit the two equivalent characterizations for this process: the first one is a time-changed classic birth and death process, whereas the second one is a Markov renewal process. Finally, we apply our main theorems to the linear model originally introduced by Orsingher and Polito [23].