In this paper, we propose a new numerical method for solvingelliptic equations in unbounded regions of ${\mathbb{R}}^n$ 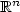 . Themethod is based on the mapping of a part of the domain into abounded region. An appropriate family of weighted spaces is usedfor describing the growth or the decay of functions at large distances. Afterexposing the main ideas of the method, we analysecarefully its convergence. Some 3D computational results are displayedto demonstrate its efficiency and its high performance.
. Themethod is based on the mapping of a part of the domain into abounded region. An appropriate family of weighted spaces is usedfor describing the growth or the decay of functions at large distances. Afterexposing the main ideas of the method, we analysecarefully its convergence. Some 3D computational results are displayedto demonstrate its efficiency and its high performance.