Elliptic hyperlogarithms
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-36
-
- Article
- Export citation
Reciprocity Laws on Algebraic Surfaces via Iterated Integrals
-
- Journal:
- Journal of K-Theory / Volume 14 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 30 September 2014, pp. 273-312
- Print publication:
- October 2014
-
- Article
- Export citation
Iterated Integrals and Higher Order Invariants
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 3 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 544-552
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Regularization and generalized double shuffle relations for $p$-adic multiple zeta values
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 5 / September 2007
- Published online by Cambridge University Press:
- 20 September 2007, pp. 1089-1107
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
NON-ABELIAN UNIPOTENT PERIODS AND MONODROMY OF ITERATED INTEGRALS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 2 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 27 January 2003, pp. 145-168
- Print publication:
- January 2003
-
- Article
- Export citation
Zeros of Iterated Integrals of Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 1 / 01 February 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 65-87
- Print publication:
- 01 February 1995
-
- Article
-
- You have access
- Export citation

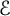
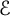
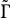
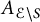
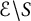
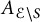
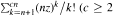 an integer) converge to pieces of a circle and of two "Szegö curves".
an integer) converge to pieces of a circle and of two "Szegö curves".
