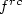Refine search
Actions for selected content:
2 results
Linear convergence in the approximationof rank-one convex envelopes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 5 / September 2004
- Published online by Cambridge University Press:
- 15 October 2004, pp. 811-820
- Print publication:
- September 2004
-
- Article
- Export citation
Optimal control approach ininverse radiative transfer problems: the problem on boundary function
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 5 / 2000
- Published online by Cambridge University Press:
- 15 August 2002, pp. 259-278
- Print publication:
- 2000
-
- Article
- Export citation