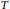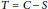Refine search
Actions for selected content:
14 results
Maximum Likelihood Solution to Factor Analysis when Some Factors are Completely Specified
-
- Journal:
- Psychometrika / Volume 36 / Issue 2 / June 1971
- Published online by Cambridge University Press:
- 01 January 2025, pp. 155-163
-
- Article
- Export citation
7 - The Second-Order Reliability Method
-
- Book:
- Structural and System Reliability
- Published online:
- 13 January 2022
- Print publication:
- 13 January 2022, pp 185-199
-
- Chapter
- Export citation
The Shifted Classical Circulant and Skew Circulant Splitting Iterative Methods for Toeplitz Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 4 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 807-815
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation
Modulus-based Synchronous Multisplitting Iteration Methods for an Implicit Complementarity Problem
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 363-375
- Print publication:
- May 2017
-
- Article
- Export citation
A Non-Krylov Subspace Method for Solving Large and Sparse Linear System of Equations
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 24 May 2016, pp. 289-314
- Print publication:
- May 2016
-
- Article
- Export citation
A Nonlocal Total Variation Model for Image Decomposition: Illumination and Reflectance
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 3 / August 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 334-355
- Print publication:
- August 2014
-
- Article
- Export citation
An Efficient Numerical Solution Method for Elliptic Problems in Divergence Form
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 6 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 327-344
- Print publication:
- June 2014
-
- Article
- Export citation
Extinction Probabilities of Branching Processes with Countably Infinitely Many Types
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1068-1082
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
An Acceleration Method for Stationary Iterative Solution to Linear System of Equations
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 4 / Issue 4 / August 2012
- Published online by Cambridge University Press:
- 03 June 2015, pp. 473-482
- Print publication:
- August 2012
-
- Article
- Export citation
A Spectral Iterative Method for the Computation of Effective Properties Of Elastically Inhomogeneous Polycrystals
-
- Journal:
- Communications in Computational Physics / Volume 11 / Issue 3 / March 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 726-738
- Print publication:
- March 2012
-
- Article
- Export citation
Quantifying Tectonic and Geomorphic Interpretations of Thermochronometer Data with Inverse Problem Theory
-
- Journal:
- Communications in Computational Physics / Volume 9 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 129-146
- Print publication:
- January 2011
-
- Article
- Export citation
An iterative procedure to solve a coupled two-fluids turbulence model
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 23 February 2010, pp. 693-713
- Print publication:
- July 2010
-
- Article
- Export citation