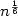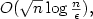1 results
Generic Primal-dual Interior Point Methods Based on a New Kernel Function
-
- Journal:
- RAIRO - Operations Research / Volume 42 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 17 May 2008, pp. 199-213
- Print publication:
- April 2008
-
- Article
- Export citation
-
In this paper we present a generic primal-dualinterior point methods (IPMs) for linear optimization in which the search direction depends on a univariate kernel function which is also used as proximity measure in the analysis of the algorithm. The proposed kernel function does not satisfy all the conditions proposed in [2].We show that the corresponding large-update algorithm improves the iteration complexity with a factor $n^{\frac16}$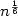
when compared with the method based on the use of the classical logarithmic barrier function. For small-update interior point methods the iteration bound is $O(\sqrt{n}\log\frac{n}{\epsilon}),$ 
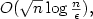which is currently the best-known bound for primal-dual IPMs.
