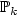A Discontinuous Galerkin method is used for to thenumerical solution of the time-domain Maxwell equations onunstructured meshes. The method relies on the choice of local basisfunctions, a centered mean approximation for the surface integralsand a second-order leap-frog scheme for advancing in time. The methodis proved to be stable for cases with either metallic or absorbingboundary conditions, for a large class of basis functions. A discrete analog of the electromagnetic energy is conserved formetallic cavities. Convergence is proved for $\mathbb{P}_k$ 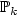 Discontinuous elements on tetrahedral meshes, as well as a discretedivergence preservation property. Promising numerical examples withlow-order elements show the potential of the method.
Discontinuous elements on tetrahedral meshes, as well as a discretedivergence preservation property. Promising numerical examples withlow-order elements show the potential of the method.