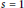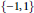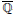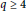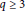1 results
On a Conjecture of Livingston
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-195
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
-
In an attempt to resolve a folklore conjecture of Erdös regarding the non-vanishing at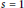
$s\,=\,1$ of the 
$L$-series attached to a periodic arithmetical function with period 
$q$ and values in 
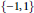$\left\{ -1,\,1 \right\}$, Livingston conjectured the 
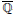$\overline{\mathbb{Q}}$-linear independence of logarithms of certain algebraic numbers. In this paper, we disprove Livingston’s conjecture for composite 
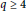$q\,\ge \,4$, highlighting that a new approach is required to settle Erdös conjecture. We also prove that the conjecture is true for prime 
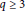$q\,\ge \,3$, and indicate that more ingredients will be needed to settle Erdös conjecture for prime 
$q$.
