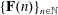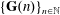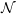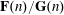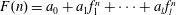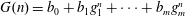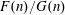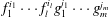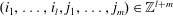4 results
COUNTING UNIONS OF SCHREIER SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 19-31
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
The Quotient Problem for Entire Functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 26 October 2018, pp. 479-489
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
ON APPROXIMATE SOLUTIONS OF SOME DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 476-481
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
On numbers n dividing the nth term of a linear recurrence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 271-289
-
- Article
-
- You have access
- Export citation