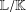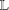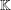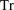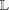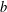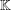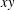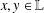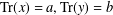Search

This paper deals with the following problem. Given a finite extension of fields 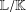$\mathbb{L}/\mathbb{K}$ and denoting the trace map from 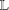$\mathbb{L}$ to 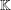$\mathbb{K}$ by 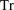$\text{Tr}$, for which elements $z$ in 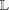$\mathbb{L}$, and $a$, 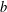$b$ in 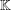$\mathbb{K}$, is it possible to write $z$ as a product 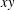$xy$, where 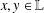$x,y\in \mathbb{L}$ with 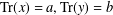$\text{Tr}(x)=a,\text{Tr}(y)=b$? We solve most of these problems for finite fields, with a complete solution when the degree of the extension is at least 5. We also have results for arbitrary fields and extensions of degrees 2, 3 or 4. We then apply our results to the study of perfect nonlinear functions, semifields, irreducible polynomials with prescribed coefficients, and a problem from finite geometry concerning the existence of certain disjoint linear sets.

A number of points are chosen at random along a line segment and used as the left end-points of lengths of fixed size. Finite sum expressions are derived for the moments of the portion of the line segment covered by one or more of the lengths. The derivation utilizes a relationship between the coverage and the busy time in an M/D/∞ queue.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

ON THE PRODUCT OF ELEMENTS WITH PRESCRIBED TRACE

The moments of coverage of a linear set

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

ON THE PRODUCT OF ELEMENTS WITH PRESCRIBED TRACE

The moments of coverage of a linear set