11 results
Asymptotic normality in t-stack sortable permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 November 2020, pp. 1062-1070
-
- Article
- Export citation
Limit theorems for some skew products with mixing base maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 August 2019, pp. 241-271
- Print publication:
- January 2021
-
- Article
- Export citation
Distance between two random k-out digraphs, with and without preferential attachment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 858-879
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Convergence results on multitype, multivariate branching random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 681-705
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Limit distributions for the number of leaves in a random forest
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 904-922
- Print publication:
- December 2002
-
- Article
- Export citation
Limit theorems for isotropic random walks on triangle buildings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-334
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Random walks and periodic continued fractions
-
- Journal:
- Advances in Applied Probability / Volume 17 / Issue 1 / March 1985
- Published online by Cambridge University Press:
- 01 July 2016, pp. 67-84
- Print publication:
- March 1985
-
- Article
- Export citation
Limit theorems for first-passage times in linear and non-linear renewal theory
-
- Journal:
- Advances in Applied Probability / Volume 16 / Issue 4 / December 1984
- Published online by Cambridge University Press:
- 01 July 2016, pp. 766-803
- Print publication:
- December 1984
-
- Article
- Export citation
Limit theorems for general size distributions
-
- Journal:
- Journal of Applied Probability / Volume 18 / Issue 1 / March 1981
- Published online by Cambridge University Press:
- 14 July 2016, pp. 139-147
- Print publication:
- March 1981
-
- Article
- Export citation
A local limit theorem for the critical age-dependent branching process
-
- Journal:
- Journal of Applied Probability / Volume 15 / Issue 1 / March 1978
- Published online by Cambridge University Press:
- 14 July 2016, pp. 46-53
- Print publication:
- March 1978
-
- Article
- Export citation
Asymptotic properties of the number of replications of a paired comparison
-
- Journal:
- Journal of Applied Probability / Volume 11 / Issue 1 / March 1974
- Published online by Cambridge University Press:
- 14 July 2016, pp. 43-52
- Print publication:
- March 1974
-
- Article
- Export citation

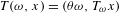


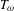

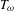


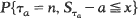 is obtained, where
is obtained, where 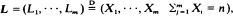 i.e.,
i.e., 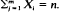 It is easy to see that our model includes the classical urn model, the Bose–Einstein urn model and the Pólya urn model as special cases. For any non-negative integer
It is easy to see that our model includes the classical urn model, the Bose–Einstein urn model and the Pólya urn model as special cases. For any non-negative integer 