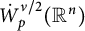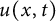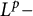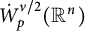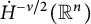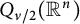3 results
Sobolev trace-type inequalities via time-space fractional heat equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivalence between logarithmic Sobolev inequality and hypercontractivity in a probability gage space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 17 December 2020, pp. 59-71
-
- Article
- Export citation
Logarithmic Sobolev inequalities for inhomogeneous Markov Semigroups
-
- Journal:
- ESAIM: Probability and Statistics / Volume 12 / 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 492-504
- Print publication:
- 2008
-
- Article
- Export citation