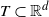1 results
Efficient conditional Monte Carlo simulations for the exponential integrals of Gaussian random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 366-383
- Print publication:
- June 2022
-
- Article
- Export citation
-
We consider a continuous Gaussian random field living on a compact set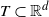
$T\subset \mathbb{R}^{d}$
. We are interested in designing an asymptotically efficient estimator of the probability that the integral of the exponential of the Gaussian process over T exceeds a large threshold u. We propose an Asmussen–Kroese conditional Monte Carlo type estimator and discuss its asymptotic properties according to the assumptions on the first and second moments of the Gaussian random field. We also provide a simulation study to illustrate its effectiveness and compare its performance with the importance sampling type estimator of Liu and Xu (2014a).
