Foreman and Weiss [Measure preserving diffeomorphisms of the torus are unclassifiable. Preprint, 2020, arXiv:1705.04414] obtained an anti-classification result for smooth ergodic diffeomorphisms, up to measure isomorphism, by using a functor 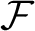 $\mathcal {F}$
(see [Foreman and Weiss, From odometers to circular systems: a global structure theorem. J. Mod. Dyn.15 (2019), 345–423]) mapping odometer-based systems,
$\mathcal {F}$
(see [Foreman and Weiss, From odometers to circular systems: a global structure theorem. J. Mod. Dyn.15 (2019), 345–423]) mapping odometer-based systems, 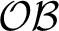 $\mathcal {OB}$
, to circular systems,
$\mathcal {OB}$
, to circular systems, 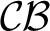 $\mathcal {CB}$
. This functor transfers the classification problem from
$\mathcal {CB}$
. This functor transfers the classification problem from 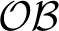 $\mathcal {OB}$
to
$\mathcal {OB}$
to 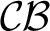 $\mathcal {CB}$
, and it preserves weakly mixing extensions, compact extensions, factor maps, the rank-one property, and certain types of isomorphisms. Thus it is natural to ask whether
$\mathcal {CB}$
, and it preserves weakly mixing extensions, compact extensions, factor maps, the rank-one property, and certain types of isomorphisms. Thus it is natural to ask whether 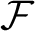 $\mathcal {F}$
preserves other dynamical properties. We show that
$\mathcal {F}$
preserves other dynamical properties. We show that 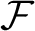 $\mathcal {F}$
does not preserve the loosely Bernoulli property by providing positive and zero-entropy examples of loosely Bernoulli odometer-based systems whose corresponding circular systems are not loosely Bernoulli. We also construct a loosely Bernoulli circular system whose corresponding odometer-based system has zero entropy and is not loosely Bernoulli.
$\mathcal {F}$
does not preserve the loosely Bernoulli property by providing positive and zero-entropy examples of loosely Bernoulli odometer-based systems whose corresponding circular systems are not loosely Bernoulli. We also construct a loosely Bernoulli circular system whose corresponding odometer-based system has zero entropy and is not loosely Bernoulli.