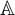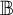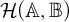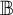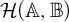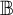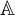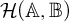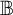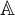For given Boolean algebras $\mathbb {A}$ and $\mathbb {B}$ we endow the space $\mathcal {H}(\mathbb {A},\mathbb {B})$ of all Boolean homomorphisms from $\mathbb {A}$ to $\mathbb {B}$ with various topologies and study convergence properties of sequences in $\mathcal {H}(\mathbb {A},\mathbb {B})$ . We are in particular interested in the situation when $\mathbb {B}$ is a measure algebra as in this case we obtain a natural tool for studying topological convergence properties of sequences of ultrafilters on $\mathbb {A}$ in random extensions of the set-theoretical universe. This appears to have strong connections with Dow and Fremlin’s result stating that there are Efimov spaces in the random model. We also investigate relations between topologies on $\mathcal {H}(\mathbb {A},\mathbb {B})$ for a Boolean algebra $\mathbb {B}$ carrying a strictly positive measure and convergence properties of sequences of measures on $\mathbb {A}$ .

A close analogue for some hypergroup measure algebras of the structure semigroup theorem of J. L. Taylor for convolution measure algebras is constructed: a structure semihypergroup representation is made for the hypergroup measure and its spectrum. This is done for those hypergroup measure algebras that satisfy a condition known as the structure-strong condition. This condition is that the norm-closure of the linear span of the spectrum of the hypergroup measure algebra is a commutative B*-algebra. Then examples of hypergroups whose measure algebras satisfy this condition are given. They include the space of B-orbits of G, where B is a finite solvable group of automorphisms on a locally compact abelian group G. (The hypergroup measure algebra may be identified with the algebra of B-invariant measures on G.) Other examples are the algebra of central measures on a compact, connected, semisimple Lie group, and the algebra of rotation invariant measures on the plane.

In this paper, we introduce the concept of topological left substantial subsemigroup of a locally compact semigroup S and prove that if T is such a subsemigroup in S and M(T) is the measure algebra of T, then M(T)* is topological left amenable iff M(S)* is topological left amenable, an extension of a similar result for discrete semigroups.