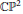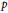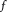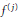Refine search
Actions for selected content:
19 results
A note on Hayman’s problem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 18 December 2024, pp. 620-627
- Print publication:
- June 2025
-
- Article
- Export citation
NOTES ON FERMAT-TYPE DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 324-335
- Print publication:
- April 2025
-
- Article
- Export citation
BOUNDS FOR FUNCTIONALS DEFINED ON A CERTAIN CLASS OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 March 2023, pp. 101-109
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iterates of meromorphic functions on escaping Fatou components
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1906-1928
- Print publication:
- December 2023
-
- Article
- Export citation
Hausdorff dimension of escaping sets of meromorphic functions II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 1471-1491
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slices of parameter space for meromorphic maps with two asymptotic values
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 99-139
- Print publication:
- January 2023
-
- Article
- Export citation
Restrictions on meromorphic solutions of Fermat type equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 08 May 2020, pp. 654-665
-
- Article
- Export citation
Division algebras of slice functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 15 March 2019, pp. 2055-2082
- Print publication:
- August 2020
-
- Article
- Export citation
SOME NORMALITY CRITERIA AND A COUNTEREXAMPLE TO THE CONVERSE OF BLOCH’S PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 238-249
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Hausdorff Dimension of Sets of Escaping Points and Escaping Parameters for Elliptic Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 30 December 2015, pp. 671-690
-
- Article
- Export citation
A Note on Planarity Stratification of Hurwitz Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 3 / 01 September 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 596-609
- Print publication:
- 01 September 2015
-
- Article
-
- You have access
- Export citation
REMARKS ON VALUE SHARING OF CERTAIN DIFFERENTIAL POLYNOMIALS OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 28 August 2014, pp. 427-443
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Integer Points of Meromorphic Functions
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 21 August 2013, pp. 367-376
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF MEROMORPHIC FUNCTIONS SHARING ONE VALUE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 04 January 2012, pp. 280-294
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
DIFFERENTIAL SUBORDINATIONS FOR CLASSES OF MEROMORPHIC p-VALENT FUNCTIONS DEFINED BY MULTIPLIER TRANSFORMATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 05 April 2011, pp. 353-368
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Ergodic properties of semi-hyperbolic functions with polynomial Schwarzian derivative
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 471-502
-
- Article
-
- You have access
- Export citation
LAMINATIONS DANS LES ESPACES PROJECTIFS COMPLEXES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 15 March 2007, pp. 67-91
- Print publication:
- January 2008
-
- Article
- Export citation
Meromorphic Functions Sharing the Same Zeros and Poles
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 6 / 01 December 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1190-1227
- Print publication:
- 01 December 2004
-
- Article
-
- You have access
- Export citation
On a class of two-dimensional nearest-neighbour random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 207-237
- Print publication:
- 1994
-
- Article
- Export citation



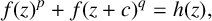
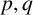
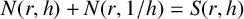
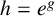

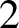
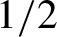
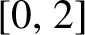
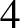
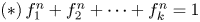
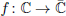 be a non-constant elliptic function. We prove that the Hausdorff dimension of the escaping set of
be a non-constant elliptic function. We prove that the Hausdorff dimension of the escaping set of