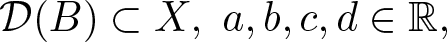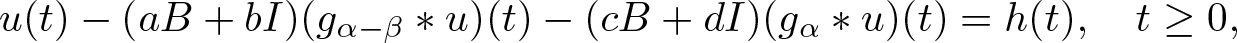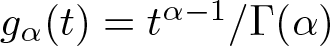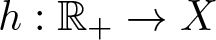9 results
Well-posedness for strongly damped abstract Cauchy problems of fractional order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-27
-
- Article
- Export citation
Local and global existence and uniqueness of solution for abstract differential equations with state-dependent argument
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 305-345
-
- Article
- Export citation
17 - Initial Value Problems for Ordinary Differential Equations
- from Part IV - Initial Value Problems for Ordinary Differential Equations
-
- Book:
- Classical Numerical Analysis
- Published online:
- 29 September 2022
- Print publication:
- 20 October 2022, pp 509-524
-
- Chapter
- Export citation
Analysis of a spatially inhomogeneous stochastic partial differential equation epidemic model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 613-636
- Print publication:
- June 2020
-
- Article
- Export citation
Numerical Approximation of Stationary Distributions for Stochastic Partial Differential Equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 858-873
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
ON PSEUDO
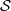 $ \mathcal{S} $-ASYMPTOTICALLY PERIODIC FUNCTIONS
$ \mathcal{S} $-ASYMPTOTICALLY PERIODIC FUNCTIONS
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 30 January 2013, pp. 238-254
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Strong stabilization of controlled vibrating systems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 08 November 2010, pp. 1144-1157
- Print publication:
- October 2011
-
- Article
- Export citation
On Some Stochastic Perturbations of Semilinear Evolution Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 3 / 01 September 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 526-533
- Print publication:
- 01 September 2010
-
- Article
-
- You have access
- Export citation
Local Solutions for Stochastic Navier Stokes Equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 34 / Issue 2 / March 2000
- Published online by Cambridge University Press:
- 15 April 2002, pp. 241-273
- Print publication:
- March 2000
-
- Article
- Export citation