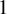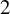The definition of subshifts of finite symbolic rank is motivated by the finite rank measure-preserving transformations which have been extensively studied in ergodic theory. In this paper, we study subshifts of finite symbolic rank as essentially minimal Cantor systems. We show that minimal subshifts of finite symbolic rank have finite topological rank, and conversely, every minimal Cantor system of finite topological rank is either an odometer or conjugate to a minimal subshift of finite symbolic rank. We characterize the class of all minimal Cantor systems conjugate to a rank-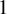 $1$ subshift and show that it is dense but not generic in the Polish space of all minimal Cantor systems. Within some different Polish coding spaces of subshifts, we also show that the rank-1 subshifts are dense but not generic. Finally, we study topological factors of minimal subshifts of finite symbolic rank. We show that every infinite odometer and every irrational rotation is the maximal equicontinuous factor of a minimal subshift of symbolic rank
$1$ subshift and show that it is dense but not generic in the Polish space of all minimal Cantor systems. Within some different Polish coding spaces of subshifts, we also show that the rank-1 subshifts are dense but not generic. Finally, we study topological factors of minimal subshifts of finite symbolic rank. We show that every infinite odometer and every irrational rotation is the maximal equicontinuous factor of a minimal subshift of symbolic rank 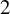 $2$, and that a subshift factor of a minimal subshift of finite symbolic rank has finite symbolic rank.
$2$, and that a subshift factor of a minimal subshift of finite symbolic rank has finite symbolic rank.