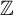Refine search
Actions for selected content:
2 results
Dynamical properties of minimal Ferenczi subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 22 February 2023, pp. 3923-3970
- Print publication:
- December 2023
-
- Article
- Export citation
On the automorphism group of minimal
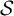 $\mathcal {S}$-adic subshifts of finite alphabet rank
$\mathcal {S}$-adic subshifts of finite alphabet rank
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 30 June 2021, pp. 2800-2822
- Print publication:
- September 2022
-
- Article
- Export citation