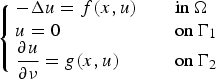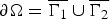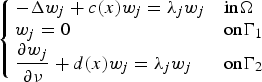1 results
Morse index and symmetry for elliptic problems with nonlinear mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 305-324
- Print publication:
- April 2019
-
- Article
- Export citation
-
We consider an elliptic problem of the type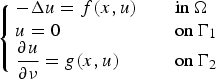
where Ω is a bounded Lipschitz domain in ℝN with a cylindrical symmetry, ν stands for the outer normal and
$$\left\{ {\matrix{ {-\Delta u = f(x,u)\quad } \hfill & {{\rm in}\,\Omega } \hfill \cr {u = 0} \hfill & {{\rm on}\,\Gamma _1} \hfill \cr {\displaystyle{{\partial u} \over {\partial \nu }} = g(x,u)} \hfill & {{\rm on}\,\Gamma _2} \hfill \cr } } \right.$$
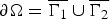$\partial \Omega = \overline {\Gamma _1} \cup \overline {\Gamma _2} $.Under a Morse index condition, we prove cylindrical symmetry results for solutions of the above problem.
As an intermediate step, we relate the Morse index of a solution of the nonlinear problem to the eigenvalues of the following linear eigenvalue problem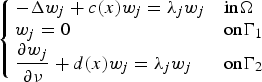
For this one, we construct sequences of eigenvalues and provide variational characterization of them, following the usual approach for the Dirichlet case, but working in the product Hilbert space L2 (Ω) × L2(Γ2).
$$\left\{ {\matrix{ {-\Delta w_j + c(x)w_j = \lambda _jw_j} \hfill & {{\rm in }\Omega } \hfill \cr {w_j = 0} \hfill & {{\rm on }\Gamma _1} \hfill \cr {\displaystyle{{\partial w_j} \over {\partial \nu }} + d(x)w_j = \lambda _jw_j} \hfill & {{\rm on }\Gamma _2} \hfill \cr } } \right.$$
