1 results
Model selection for (auto-)regression with dependent data
-
- Journal:
- ESAIM: Probability and Statistics / Volume 5 / 2001
- Published online by Cambridge University Press:
- 15 August 2002, pp. 33-49
- Print publication:
- 2001
-
- Article
- Export citation
-
In this paper, we study the problem of non parametric estimationof an unknown regression function from dependent data withsub-Gaussian errors. As a particular case, we handle theautoregressive framework. For this purpose, we consider acollection of finite dimensional linear spaces (e.g. linear spacesspanned by wavelets or piecewise polynomials on a possiblyirregular grid) and we estimate the regression function by aleast-squares estimator built on a data driven selected linearspace among the collection. This data driven choice is performedvia the minimization of a penalized criterion akin to the Mallows'C p . We state non asymptotic risk bounds for our estimator insome ${\mathbb{L}}_2$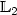
-norm and we show that it is adaptive in the minimaxsense over a large class of Besov balls of the form Bα,p,∞(R) with p ≥ 1.
