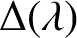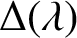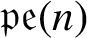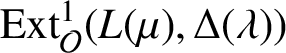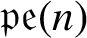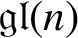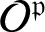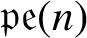Refine search
Actions for selected content:
16 results
Evaluation of Pediatric Triage Decisions Using the SALT (Sort, Assess, Life-saving Intervention, Treatment/Transport) Triage System across Training Levels
-
- Journal:
- Disaster Medicine and Public Health Preparedness / Volume 19 / 2025
- Published online by Cambridge University Press:
- 04 December 2025, e340
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Appendix E - Complexes and Homology
- from Appendices
-
- Book:
- Polygraphs: From Rewriting to Higher Categories
- Published online:
- 18 March 2025
- Print publication:
- 03 April 2025, pp 584-594
-
- Chapter
- Export citation
5 - Modularity
- from II - The Never-Ending Debate
-
- Book:
- A Mind for Language
- Published online:
- 13 October 2023
- Print publication:
- 21 September 2023, pp 130-150
-
- Chapter
- Export citation
8 - Modules
-
- Book:
- Algebraic Number Theory for Beginners
- Published online:
- 28 July 2022
- Print publication:
- 11 August 2022, pp 171-188
-
- Chapter
- Export citation
Chapter 11 - TBT-S Neurobiology Psychoeducation Module
- from Section 3 - TBT-S Treatment Interventions
-
- Book:
- Temperament Based Therapy with Support for Anorexia Nervosa
- Published online:
- 31 March 2022
- Print publication:
- 21 April 2022, pp 50-56
-
- Chapter
- Export citation
SOME HOMOLOGICAL PROPERTIES OF CATEGORY
 $\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
$\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 21 January 2022, pp. 50-77
- Print publication:
- February 2023
-
- Article
- Export citation
10 - Course Structure
- from Create
-
- Book:
- The New Roadmap for Creating Online Courses
- Published online:
- 26 May 2020
- Print publication:
- 11 June 2020, pp 143-158
-
- Chapter
- Export citation
Thermal characterisation analysis and modelling techniques for CubeSat-sized spacecrafts
-
- Journal:
- The Aeronautical Journal / Volume 121 / Issue 1246 / December 2017
- Published online by Cambridge University Press:
- 17 October 2017, pp. 1858-1878
-
- Article
- Export citation
ON MAXIMAL ESSENTIAL EXTENSIONS OF RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 29 October 2010, pp. 329-337
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
DIRECT SUMS OF INFINITELY MANY KERNELS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 23 November 2010, pp. 199-214
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Equivalence of consequence relations: an order-theoretic and categorical perspective
-
- Journal:
- The Journal of Symbolic Logic / Volume 74 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 12 March 2014, pp. 780-810
- Print publication:
- September 2009
-
- Article
- Export citation
FINITELY GENERATED COTORSION MODULES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 44 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 20 January 2009, pp. 143-152
-
- Article
-
- You have access
- Export citation
INDECOMPOSABLE NON-HOLONOMIC $\mathcal{D}$-MODULES IN DIMENSION $2$
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 46 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 04 July 2003, pp. 341-355
-
- Article
-
- You have access
- Export citation
Length theorems for the general linear group of a module over a local ring
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 1 / February 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 122-131
- Print publication:
- February 1989
-
- Article
-
- You have access
- Export citation
Bounding the stochastic performance of continuum structure functions. I
-
- Journal:
- Journal of Applied Probability / Volume 23 / Issue 3 / September 1986
- Published online by Cambridge University Press:
- 14 July 2016, pp. 660-669
- Print publication:
- September 1986
-
- Article
- Export citation
A Problem on Relative Projectivity for Abelian Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 1 / 01 March 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 114-122
- Print publication:
- 01 March 1986
-
- Article
-
- You have access
- Export citation