2 results
Oscillations of higher order neutral differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-81
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
-
Some new oscillation criteria for higher order neutral functional differential equations of the form
n is even, are established.
Oscillations in Higher-Order Neutral Differential Equations
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 1 / 01 February 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 132-158
- Print publication:
- 01 February 1993
-
- Article
-
- You have access
- Export citation
-
Consider the n-th order (n ≥ 1 ) neutral differential equation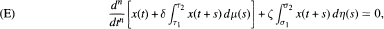
where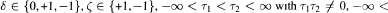 
σ1 < σ 2 < ∞ and μ and η are increasing real-valued functions on [Ƭ1, Ƭ2] and [σ1, σ2] respectively. The function μ is assumed to be not constant on [Ƭ1, Ƭ2] and [Ƭ1, Ƭ2] for every Ƭ ∈ (Ƭ1, Ƭ2) similarly, for each σ ∈ (σ1, σ2), it is supposed that r\ is not constant on [σ1 , σ] and [σ, σ2]. Under some mild restrictions on Ƭ1,- and σ1, (ι = 1,2), it is proved that all solutions of (E) are oscillatory if and only if the characteristic equation 
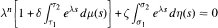of (E) has no real roots.
σ1 < σ 2 < ∞ and 
