1 results
On Non-Archimedean Curves Omitting Few Components and their Arithmetic Analogues
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 1 / 01 February 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 130-142
- Print publication:
- 01 February 2017
-
- Article
-
- You have access
- Export citation
-
Let
$\mathbf{k}$ be an algebraically closed field complete with respect to a non-Archimedean absolute value of arbitrary characteristic. Let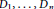 
${{D}_{1}},...,\,{{D}_{n}}$ be effective nef divisors intersecting transversally in an 
$n$-dimensional nonsingular projective variety 
$X$. We study the degeneracy of non-Archimedean analytic maps from $\mathbf{k}$ into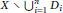 
$X\,\backslash \,\cup _{i=1}^{n}\,{{D}_{i}}$ under various geometric conditions. When $X$ is a rational ruled surface and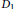 
${{D}_{1}}$ and 
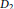${{D}_{2}}$ are ample, we obtain a necessary and sufficient condition such that there is no non-Archimedean analytic map from $\mathbf{k}$ into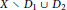 
$X\,\backslash \,{{D}_{1}}\,\cup \,{{D}_{2}}$. Using the dictionary between non-Archimedean Nevanlinna theory and Diophantine approximation that originated in earlier work with T. T. H. An, we also study arithmetic analogues of these problems, establishing results on integral points on these varieties over 
$\mathbb{Z}$ or the ring of integers of an imaginary quadratic field.
