We present a finite volume method based on the integration of the Laplaceequation on both the cells of a primal almost arbitrary two-dimensionalmesh and those of adual mesh obtained by joining the centers of the cells of the primal mesh.The key ingredient is the definition of discrete gradient and divergenceoperators verifying a discrete Green formula.This method generalizes an existing finite volume method thatrequires “Voronoi-type” meshes.We show the equivalence of this finite volume method with a non-conformingfinite element method with basis functions being P 1 on the cells,generally called “diamond-cells”, of a third mesh. Under geometrical conditions on these diamond-cells, we prove a first-order convergence both in the $\xHone_0$ 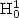 normand in the L² norm. Superconvergence results are obtained on certain types of homothetically refined grids. Finally, numerical experiments confirm these results and also show second-order convergencein the L² norm on general grids.They also indicate that this method performs particularly well for the approximationof the gradient of the solution, and may be used on degenerating triangular grids.An example of application on non-conforming locally refined grids is given.
normand in the L² norm. Superconvergence results are obtained on certain types of homothetically refined grids. Finally, numerical experiments confirm these results and also show second-order convergencein the L² norm on general grids.They also indicate that this method performs particularly well for the approximationof the gradient of the solution, and may be used on degenerating triangular grids.An example of application on non-conforming locally refined grids is given.