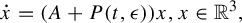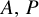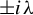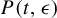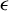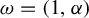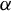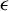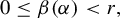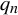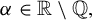We consider the system 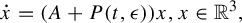 $\dot {x}=(A+ P(t,\epsilon )) x, x\in \mathbb {R}^{3}, $ where
$\dot {x}=(A+ P(t,\epsilon )) x, x\in \mathbb {R}^{3}, $ where 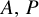 $A, P$ are both three-dimensional skew symmetric matrices, A is a constant matrix with eigenvalues
$A, P$ are both three-dimensional skew symmetric matrices, A is a constant matrix with eigenvalues 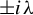 $\pm i\unicode{x3bb} $ and 0,
$\pm i\unicode{x3bb} $ and 0, 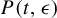 $P(t,\epsilon )$ is
$P(t,\epsilon )$ is  $C^{m}(m=0,1)$-smooth in
$C^{m}(m=0,1)$-smooth in 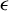 $\epsilon $ and analytic quasi-periodic with respect to t with basic frequencies
$\epsilon $ and analytic quasi-periodic with respect to t with basic frequencies 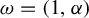 $\omega =(1,\alpha )$, with
$\omega =(1,\alpha )$, with 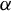 $\alpha $ being irrational, and
$\alpha $ being irrational, and 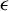 $\epsilon $ is a small parameter. Under some non-resonant conditions about the basic frequencies and the eigenvalues of the constant matrix and without any non-degeneracy condition, it is proved that for many sufficiently small parameters, this system can be reduced to a rotation system. Furthermore, if the basic frequencies satisfy that
$\epsilon $ is a small parameter. Under some non-resonant conditions about the basic frequencies and the eigenvalues of the constant matrix and without any non-degeneracy condition, it is proved that for many sufficiently small parameters, this system can be reduced to a rotation system. Furthermore, if the basic frequencies satisfy that 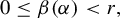 $ 0\leq \beta (\alpha ) < r,$ where
$ 0\leq \beta (\alpha ) < r,$ where  $\beta (\alpha )=\limsup \nolimits _{n\rightarrow \infty } {\ln q_{n+1}}/{q_{n}},$
$\beta (\alpha )=\limsup \nolimits _{n\rightarrow \infty } {\ln q_{n+1}}/{q_{n}},$ 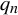 $q_{n}$ is the sequence of denominations of the best rational approximations for
$q_{n}$ is the sequence of denominations of the best rational approximations for 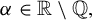 $\alpha \in \mathbb {R} \setminus \mathbb {Q},$ r is the initial radius of analytic domain, it is proved that for many sufficiently small parameters, this system can be reduced to a constant system.
$\alpha \in \mathbb {R} \setminus \mathbb {Q},$ r is the initial radius of analytic domain, it is proved that for many sufficiently small parameters, this system can be reduced to a constant system.