1 results
Lyapunov optimization for non-generic one-dimensional expanding Markov maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2571-2592
- Print publication:
- September 2020
-
- Article
- Export citation
-
For a non-generic, yet dense subset of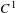
$C^{1}$ expanding Markov maps of the interval we prove the existence of uncountably many Lyapunov optimizing measures which are ergodic, fully supported and have positive entropy. These measures are equilibrium states for some Hölder continuous potentials. We also prove the existence of another non-generic dense subset for which the optimizing measure is unique and supported on a periodic orbit. A key ingredient is a new 
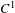$C^{1}$ perturbation theorem which allows us to interpolate between expanding Markov maps and the shift map on a finite number of symbols.
