We consider the boundary-value problem

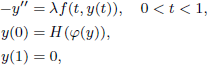
where H: [0,+∞) → ℝ and f : [0, 1] × ℝ → ℝ are continuous and λ > 0 is a parameter. We show that if H satisfies a boundedness condition on a specified compact set, then this, together with an assumption that H is either affine or superlinear at +∞, implies existence of at least one positive solution to the problem, even in the case where we impose no growth conditions on f. Finally, since it can hold that f(t, y) < 0 for all (t, y) ∈ [0, 1]×ℝ, the semipositone problem is included as a special case of the existence result.

In this paper we consider the existence of a positive solution to boundary-value problems with non-local nonlinear boundary conditions, the archetypical example being −y″(t) = λf(t,y(t)), t ∈ (0, 1), y(0) = H(φ(y)), y(1) = 0. Here, H is a nonlinear function, λ > 0 is a parameter and φ is a linear functional that is realized as a Lebesgue—Stieltjes integral with signed measure. By requiring φ to decompose in a certain way, we show that this problem has at least one positive solution for each λ ∈ (0, λ0), for a number λ0 > 0 that is explicitly computable. We also give a separate result that holds for all λ > 0.