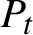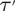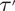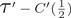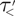4 results
Equidistribution of horospheres in non-positive curvature
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 28 October 2021, pp. 460-479
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting closed geodesics in a compact rank-one locally CAT(0) space
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 27 August 2021, pp. 1220-1251
- Print publication:
- March 2022
-
- Article
- Export citation
Generalized small cancellation conditions, non-positive curvature and diagrammatic reducibility
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 March 2021, pp. 545-566
- Print publication:
- June 2022
-
- Article
- Export citation
10 - Applications to Algebra, Geometry and Topology
- from Part Three - Differential Operators
-
- Book:
- Higher Index Theory
- Published online:
- 11 June 2020
- Print publication:
- 02 July 2020, pp 393-416
-
- Chapter
- Export citation