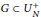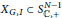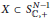Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Login Alert

Cancel

Log in

×

Register

Log In

(0) Cart

Back to search results

Home
Search

Search Results

Refine search

Access:

Only show content I have access to (1)

Content type:

Articles (1)

Author:

Publication date:

Over 3 years (1)

From year:

To year:

Apply From and To filters

Subject: Show more

Mathematics (1)

Actions for selected content:

Select all | Deselect all

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Search Title: required Please provide a title, maximum of 40 characters.

Cancel

×

1 results

Tannakian Duality for Affine Homogeneous Spaces
Teodor Banica
Journal:

Canadian Mathematical Bulletin / Volume 61 / Issue 3 / 01 September 2018

Published online by Cambridge University Press:

20 November 2018, pp. 483-494

Print publication:

01 September 2018
- Article
- - You have access
- PDF
- Export citation
Associated with any closed quantum subgroup $G\,\subset \,U_{N}^{+}$ and any index set $I\,\subset \,\{1,\,.\,.\,.\,,\,N\}$ is a certain homogeneous space ${{X}_{G,I}}\subset S_{\mathbb{C},+}^{N-1},$ called an affine homogeneous space. Using Tannakian duality methods, we discuss the abstract axiomatization of the algebraic manifolds $X\subset S_{\mathbb{C},+}^{N-1}$ that can appear in this way.