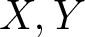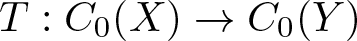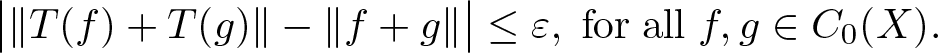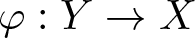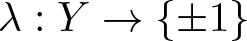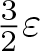Search

Only show content I have access to (0)

Articles (1)

Last 6 months (1)

Last 12 months (1)

Last 3 years (1)

From year:

To year:

Apply

Mathematics (1)

norm-additive maps

Proceedings of the Edinburgh Mathematical Society (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services Please confirm that you accept the terms of use.

×

Let 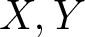$X, Y$ be two locally compact Hausdorff spaces and 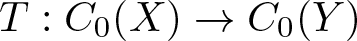$T:C_0(X)\rightarrow C_0(Y)$ be a standard surjective ɛ-norm-additive map, i.e.

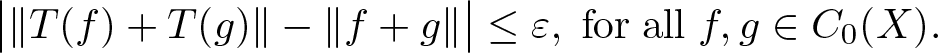\begin{equation*}\big|\|T(f)+T(g)\|-\|f+g\|\big|\leq \varepsilon,\;{\rm for\;all}\; f, g\in C_0(X).\end{equation*}

$\begin{equation*}\big|\|T(f)+T(g)\|-\|f+g\|\big|\leq \varepsilon,\;{\rm for\;all}\; f, g\in C_0(X).\end{equation*}$

Then there exist a homeomorphism 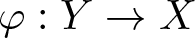$\varphi:Y\rightarrow X$ and a continuous function 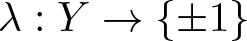$\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that

\begin{equation*}|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\;y\in Y,\;f\in C_0(X).\end{equation*}

$\begin{equation*}|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\;y\in Y,\;f\in C_0(X).\end{equation*}$

The estimate ‘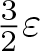 $\frac{3}{2}\varepsilon$ ’ is optimal. And this result can be regarded as a new nonlinear extension of the Banach–Stone theorem.

Search Results

Refine search

Refine search

Actions for selected content:

1 results

Perturbations of norm-additive maps between continuous function spaces

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

1 results

Perturbations of norm-additive maps between continuous function spaces