Closure phase is the phase of a closed-loop product of spatial coherences formed by a 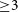${\ge}3$ -element interferometer array. Its invariance to phase corruption attributable to individual array elements acquired during the propagation and the measurement processes, subsequent calibration, and errors therein, makes it a valuable tool in interferometry applications that otherwise require high-accuracy phase calibration. However, its understanding has remained mainly mathematical and limited to the aperture plane (Fourier dual of the image plane). Here, we present a geometrical, image domain view of closure phase, which until now has been lacking. Using the principal triangle in a 3-element interference image formed by a triad of interferometer elements, we show that the properties of closure phase, particularly its invariance to multiplicative element-based corruption factors (even of a large magnitude) and to translation, are intricately related to the conserved properties of the triangle, namely, its shape, orientation, and size, which is referred herein as the ‘shape-orientation-size (SOS) conservation principle’. In the absence of a need for element-based amplitude calibration of the interferometer array (as is typical in optical interferometry), the principal triangle in any 3-element interference image formed from phase-uncalibrated spatial coherences is still a true and uncorrupted representation of the source object’s morphology, except for a possible shift. Based on this knowledge of the triangle SOS conservation principle, we present two geometric methods to measure the closure phase directly from a simple 3-element interference image (without requiring an aperture-plane view): (i) the closure phase is directly measurable from any one of the triangle’s heights, and (ii) the squared closure phase is proportional to the product of the areas enclosed by the triad of array elements and the principal triangle in the aperture and image planes, respectively. We validate the geometric understanding of closure phase in the image plane using observations with the Karl G. Jansky Very Large Array, and the Event Horizon Telescope. These results verify the SOS conservation principle across a wide range of radio interferometric conditions. This geometric insight can be potentially valuable to other interferometric applications, such as optical interferometry. We also generalise these geometric relationships to an N-element interferometer.