1 results
Orthogonal Bundles and Skew-Hamiltonian Matrices
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 5 / 01 October 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-989
- Print publication:
- 01 October 2015
-
- Article
-
- You have access
- Export citation
-
Using properties of skew-Hamiltonian matrices and classic connectedness results, we prove that the moduli space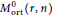
$M_{\text{ort}}^{0}\left( r,\,n \right)$ of stable rank 
$r$ orthogonal vector bundles on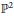 
${{\mathbb{P}}^{2}}$, with Chern classes 
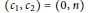$\left( {{c}_{1}},\,{{c}_{2}} \right)\,=\,\left( 0,\,n \right)$ and trivial splitting on the general line, is smooth irreducible of dimension 
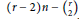$\left( r-2 \right)n\,-\,\left( _{2}^{r} \right)$ for 
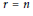$r\,=\,n$ and 
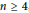$n\,\ge \,4$, and 
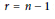$r\,=\,n-1$ and 
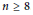$n\,\ge \,8$. We speculate that the result holds in greater generality.
