 $\mathcal {L}$-invariants and Fontaine–Mazur
$\mathcal {L}$-invariants and Fontaine–Mazur  $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
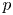 $p$-adic monodromy theorem for de Rham local systems
$p$-adic monodromy theorem for de Rham local systems
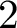 $2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE
$2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE 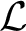 $\mathcal L$-INVARIANT
$\mathcal L$-INVARIANT
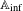 $\mathbb{A}_{\text{inf}}$ IS INFINITE DIMENSIONAL
$\mathbb{A}_{\text{inf}}$ IS INFINITE DIMENSIONAL
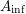 $A_{\text{inf}}$-cohomology in the semistable case
$A_{\text{inf}}$-cohomology in the semistable case
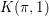 $K({\it\pi},1)$-neighborhoods and comparison theorems
$K({\it\pi},1)$-neighborhoods and comparison theorems