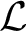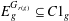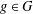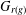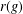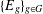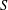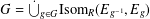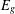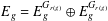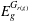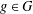3 results
ON EXTENSIONS OF PARTIAL ISOMORPHISMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 July 2020, pp. 416-435
- Print publication:
- March 2022
-
- Article
- Export citation
A CHARACTERISATION FOR A GROUPOID GALOIS EXTENSION USING PARTIAL ISOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 59-68
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
POSITIONAL STRATEGIES IN LONG EHRENFEUCHT–FRAÏSSÉ GAMES
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 13 March 2015, pp. 285-300
- Print publication:
- March 2015
-
- Article
- Export citation