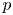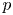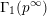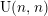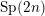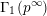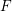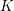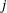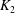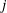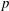4 results
The smooth locus in infinite-level Rapoport–Zink spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 03 November 2020, pp. 1846-1872
- Print publication:
- September 2020
-
- Article
- Export citation
Shimura varieties at level
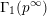 $\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
$\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1152-1230
- Print publication:
- June 2020
-
- Article
- Export citation
A motivic version of the theorem of Fontaine and Wintenberger
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 38-88
- Print publication:
- January 2019
-
- Article
- Export citation
Ramification theory and perfectoid spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 03 April 2014, pp. 798-834
- Print publication:
- May 2014
-
- Article
- Export citation