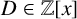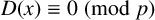2 results
SOLVABILITY OF A SYSTEM OF POLYNOMIAL EQUATIONS MODULO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 404-407
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLUTIONS TO POLYNOMIAL CONGRUENCES IN WELL-SHAPED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 435-447
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation