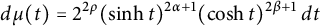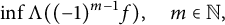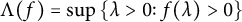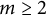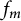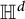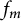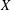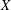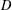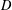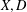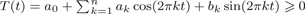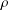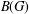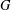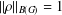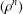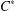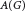We consider direct and inverse Jacobi transforms with measures 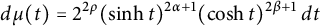 $$\begin{align*}d\mu(t)=2^{2\rho}(\operatorname{sinh} t)^{2\alpha+1}(\operatorname{cosh} t)^{2\beta+1}\,dt\end{align*}$$
$$\begin{align*}d\mu(t)=2^{2\rho}(\operatorname{sinh} t)^{2\alpha+1}(\operatorname{cosh} t)^{2\beta+1}\,dt\end{align*}$$ $$\begin{align*}d\sigma(\lambda)=(2\pi)^{-1}\Bigl|\frac{2^{\rho-i\lambda}\Gamma(\alpha+1)\Gamma(i\lambda)} {\Gamma((\rho+i\lambda)/2)\Gamma((\rho+i\lambda)/2-\beta)}\Bigr|^{-2}\,d\lambda,\end{align*}$$
$$\begin{align*}d\sigma(\lambda)=(2\pi)^{-1}\Bigl|\frac{2^{\rho-i\lambda}\Gamma(\alpha+1)\Gamma(i\lambda)} {\Gamma((\rho+i\lambda)/2)\Gamma((\rho+i\lambda)/2-\beta)}\Bigr|^{-2}\,d\lambda,\end{align*}$$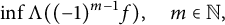 $$\begin{align*}\inf\Lambda((-1)^{m-1}f), \quad m\in \mathbb{N}, \end{align*}$$
$$\begin{align*}\inf\Lambda((-1)^{m-1}f), \quad m\in \mathbb{N}, \end{align*}$$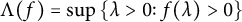 $\Lambda (f)=\sup \,\{\lambda>0\colon f(\lambda )>0\}$ and the infimum is taken over all nontrivial even entire functions f of exponential type that are Jacobi transforms of positive measures with supports on an interval. Here, if
$\Lambda (f)=\sup \,\{\lambda>0\colon f(\lambda )>0\}$ and the infimum is taken over all nontrivial even entire functions f of exponential type that are Jacobi transforms of positive measures with supports on an interval. Here, if 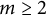 $m\ge 2$, then we additionally assume that
$m\ge 2$, then we additionally assume that  $\int _{0}^{\infty }\lambda ^{2k}f(\lambda )\,d\sigma (\lambda )=0$ for
$\int _{0}^{\infty }\lambda ^{2k}f(\lambda )\,d\sigma (\lambda )=0$ for  $k=0,\dots ,m-2$.
$k=0,\dots ,m-2$.
We prove that admissible functions for this problem are positive-definite with respect to the inverse Jacobi transform. The solution of Logan’s problem was known only when  $\alpha =\beta =-1/2$. We find a unique (up to multiplication by a positive constant) extremizer
$\alpha =\beta =-1/2$. We find a unique (up to multiplication by a positive constant) extremizer 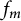 $f_m$. The corresponding Logan problem for the Fourier transform on the hyperboloid
$f_m$. The corresponding Logan problem for the Fourier transform on the hyperboloid 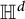 $\mathbb {H}^{d}$ is also solved. Using the properties of the extremizer
$\mathbb {H}^{d}$ is also solved. Using the properties of the extremizer 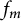 $f_m$ allows us to give an upper estimate of the length of a minimal interval containing not less than n zeros of positive definite functions. Finally, we show that the Jacobi functions form the Chebyshev systems.
$f_m$ allows us to give an upper estimate of the length of a minimal interval containing not less than n zeros of positive definite functions. Finally, we show that the Jacobi functions form the Chebyshev systems.