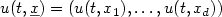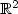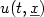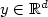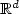1 results
Positivity of the density for the stochasticwave equation in two spatial dimensions
-
- Journal:
- ESAIM: Probability and Statistics / Volume 7 / March 2003
- Published online by Cambridge University Press:
- 15 May 2003, pp. 89-114
- Print publication:
- March 2003
-
- Article
- Export citation
-
We consider the random vector $u(t,\underlinex)=(u(t,x_1),\dots,u(t,x_d))$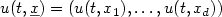
, where t > 0, x1,...,xd aredistinct points of $\mathbb{R}^2$ 
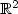and u denotes the stochastic process solution to a stochastic waveequation driven bya noise white in time and correlated in space. In a recent paper byMillet and Sanz–Solé[10], sufficient conditions are given ensuring existence andsmoothness ofdensity for $u(t,\underline x)$ 
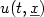. We study here the positivity of suchdensity. Usingtechniques developped in [1] (see also [9]) basedon Analysis on anabstract Wiener space, we characterize the set of points $y\in\mathbb{R}^d$ 
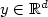where the density ispositive and we prove that, under suitable assumptions, this set is $\mathbb{R}^d$ 
.
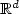