We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Minimal models of a Boolean formula play a pivotal role in various reasoning tasks. While previous research has primarily focused on qualitative analysis over minimal models; our study concentrates on the quantitative aspect, specifically counting of minimal models. Exact counting of minimal models is strictly harder than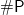 
$\#\mathsf{P}$, prompting our investigation into establishing a lower bound for their quantity, which is often useful in related applications. In this paper, we introduce two novel techniques for counting minimal models, leveraging the expressive power of answer set programming: the first technique employs methods from knowledge compilation, while the second one draws on recent advancements in hashing-based approximate model counting. Through empirical evaluations, we demonstrate that our methods significantly improve the lower bound estimates of the number of minimal models, surpassing the performance of existing minimal model reasoning systems in terms of runtime.
