The notion of recurrent fractal interpolation functions (RFIFs) was introduced by Barnsley et al. [‘Recurrent iterated function systems’, Constr. Approx. 5 (1989), 362–378]. Roughly speaking, the graph of an RFIF is the invariant set of a recurrent iterated function system on 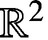 $\mathbb {R}^2$. We generalise the definition of RFIFs so that iterated functions in the recurrent system need not be contractive with respect to the first variable. We obtain the box dimensions of all self-affine RFIFs in this general setting.
$\mathbb {R}^2$. We generalise the definition of RFIFs so that iterated functions in the recurrent system need not be contractive with respect to the first variable. We obtain the box dimensions of all self-affine RFIFs in this general setting.