We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let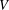 
$V$ be a vector space and let 
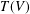$T(V)$ denote the semigroup (under composition) of all linear transformations from 
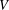$V$ into 
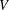$V$. For a fixed subspace 
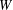$W$ of 
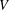$V$, let 
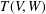$T(V,W)$ be the semigroup consisting of all linear transformations from 
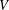$V$ into 
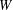$W$. In 2008, Sullivan [‘Semigroups of linear transformations with restricted range’, Bull. Aust. Math. Soc.77(3) (2008), 441–453] proved that is the largest regular subsemigroup of 
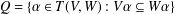$$\begin{eqnarray}\displaystyle Q=\{\unicode[STIX]{x1D6FC}\in T(V,W):V\unicode[STIX]{x1D6FC}\subseteq W\unicode[STIX]{x1D6FC}\} & & \displaystyle \nonumber\end{eqnarray}$$
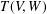$T(V,W)$ and characterized Green’s relations on 
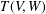$T(V,W)$. In this paper, we determine all the maximal regular subsemigroups of 
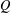$Q$ when 
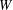$W$ is a finite-dimensional subspace of 
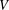$V$ over a finite field. Moreover, we compute the rank and idempotent rank of 
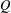$Q$ when 
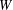$W$ is an 
$n$-dimensional subspace of an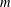 
$m$-dimensional vector space 
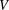$V$ over a finite field 
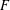$F$.
