1 results
Balancing the stations of a self service “bike hire” system
-
- Journal:
- RAIRO - Operations Research / Volume 45 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 10 May 2011, pp. 37-61
- Print publication:
- January 2011
-
- Article
- Export citation
-
This paper is motivated by operating self service transport systemsthat flourish nowadays. In cities where such systems have been setup with bikes, trucks travel to maintain a suitable number of bikesper station.It is natural to study a version of the C-delivery TSP defined byChalasani and Motwani in which, unlike their definition, C is partof the input: each vertex v of a graph G=(V,E) has a certainamount xv of a commodity and wishes to have an amount equal toyv (we assume that $\sum_{v\in V}x_v=\sum_{v\in V}y_v$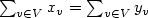
and allquantities are assumed to be integers); given a vehicle of capacityC, find a minimal route that balances all vertices, that is,that allows to have an amount yv of the commodity on each vertexv.This paper presents among other things complexity results, lowerbounds, approximation algorithms, and a polynomial algorithm whenG is a tree.
