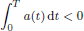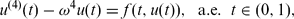2 results
Pairs of positive periodic solutions of nonlinear ODEs with indefinite weight: a topological degree approach for the super–sublinear case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 449-474
- Print publication:
- June 2016
-
- Article
- Export citation
MULTIPLE POSITIVE SOLUTIONS OF RESONANT AND NON-RESONANT NON-LOCAL FOURTH-ORDER BOUNDARY VALUE PROBLEMS
-
- Journal:
- Glasgow Mathematical Journal / Volume 54 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 December 2011, pp. 225-240
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation

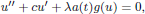
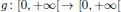 is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when
is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when